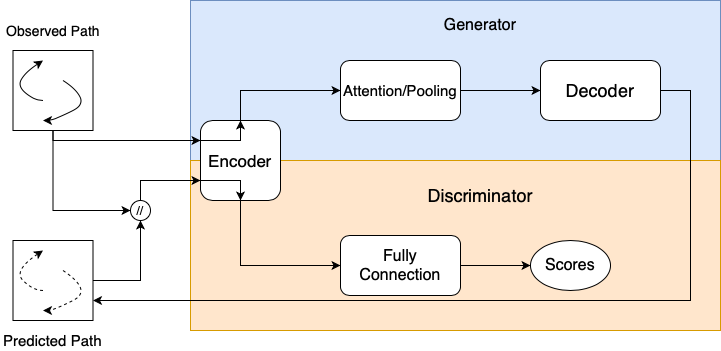
Overview
Predicting pedestrians’ future trajectories is challenging especially when their destinations are unknown. Many factors may increase the complexity of trajectories such as human-human interactions, surrounding environment and individual decisions. Nevertheless, pedestrians tend to follow social rules to adjust their paths to avoid collisions with their surrounding pedestrians or obstacles. These rules form social forces [1] that navigate pedestrians and can give some clues to predict future movement. Earlier methods statistically handcraft social features or build Long-Short Term Memory (LSTM) models [2] to predict future paths.
Stochastic models have recently been developed to generate multiple plausible routes for each pedestrian, most of which follow the encoder-decoder structure as shown in Fig. 1. Among the stochastic models, Social GAN [3], SoPhie [4], Social Ways [5] and Social BiGAT [6] incorporate the GAN architecture [7], which has a discriminator to distinguish whether a path is real or fake to assist with predicting a distribution conditioned on observed paths. In particular, Social GAN and SoPhie use the LSTM-based GANs, Social Ways uses InfoGAN [8] and Social BiGAT integrates BicycleGAN [9]. These GAN-based models achieve excellent performance on multiple datasets. There are also some non-GAN based models [10], [11] that remove the discriminator but incorporate graphs for further improvement. For example, SGAT [10] uses the Graph Attention Network [12] in the encoder to capture the interaction between pedestrians.
Social GAN follows the training process that repeatedly updates the discriminator using $L_D$ then the generator using $λL_{L2} + (1 − λ)L_G$. Initially, $L_{L_2}$ dominates the total losses (10 times of $L_G$) to create new trajectories with convincing direction and speed. Then, with the convergence of $L_{L2}, L_G$ starts to control the generated trajectories, which results in a limited span of distribution. This phenomenon is indicated in [13] as well. Although further training helps spread the trajectories to a suitable distribution, the generated trajectories tend to divert considerably from the ground truths. Therefore, the prediction performance in terms of ADE and FDE at around 100 epochs is actually better than that at 200 epochs even though the distribution is more realistic qualitatively at 200 epochs.
A plausible explanation is that, different from image tasks, temporal data generation is hard for GAN. If the decoder fails to generate accurate predictions at previous time steps, the future steps may follow such results to generate new inac- curate predictions. For stochastic models, both generator and discriminator have their own RNNs to encode the embedded human trajectories, but they aim to handle different tasks: the generator uses those features to generate future paths while the discriminator attempts to evaluate the generated path. Therefore, it is challenging to ensure that the RNNs in generator and discriminator are successfully trained and correlated with each other.
Therefore, we propose a simpler solution that the discriminator shares parameters of the encoder with the generator: each time the discriminator needs to extract trajectory features, it uses the encoder pre-trained by the generator. Then, the generator can well train its encoder due to the $L_{L_2}$ correction. In addition, because the discriminator only needs to train its fully connected layers that follow a feedforward structure, the model complexity decreases and hence the training becomes more stable.
| SGAN | SGAN-SE | FSGAN | SGAT-GAN | SGAT-SE | |
|---|---|---|---|---|---|
| ETH | 0.81/1.52 | 0.63/1.13 | 0.68/1.16 | 0.70/1.35 | 0.61/1.06 |
| HOTEL | 0.48/1.03 | 0.39/0.79 | 0.43/0.89 | 0.37/0.67 | 0.43/0.91 |
| UNIV | 0.60/1.26 | 0.53/1.15 | 0.54/1.14 | 0.59/1.23 | 0.50/1.19 |
| ZARA1 | 0.34/0.69 | 0.34/0.70 | 0.35/0.71 | 0.35/0.69 | 0.34/0.70 |
| ZARA2 | 0.42/0.84 | 0.36/0.61 | 0.32/0.67 | 0.31/0.64 | 0.36/0.78 |
Reference
-
D.HelbingandP.Molna ́r,“Socialforcemodelforpedestriandynamics.” Physical review. E, Statistical physics, plasmas, fluids, and related interdisciplinary topics, vol. 51, no. 5, pp. 4282–4286, 1995.
-
A. Alahi, K. Goel, V. Ramanathan, A. Robicquet, F.-F. Li, and S. Savarese, “Social LSTM: Human trajectory prediction in crowded spaces,” in CVPR, 2016.
-
A. Gupta, J. Johnson, L. Fei-Fei, S. Savarese, and A. Alahi, “Social GAN: Socially acceptable trajectories with generative adversarial net- works,” in CVPR, 2018.
-
A.Sadeghian,V.Kosaraju,A.Sadeghian,N.Hirose,H.Rezatofighi,and S. Savarese, “SoPhie: An attentive gan for predicting paths compliant to social and physical constraints,” in CVPR, 2019.
-
J. Amirian, J.-B. Hayet, and J. Pettre ́, “Social ways: Learning multi- modal distributions of pedestrian trajectories with gans,” in CVPRW, 2019.
-
V. Kosaraju, A. Sadeghian, R. Mart ́ın-Mart ́ın, I. D. Reid, S. H. Rezatofighi, and S. Savarese, “Social-BiGAT: Multimodal trajectory forecasting using Bicycle-GAN and graph attention networks,” in NeurIPS, 2019.
-
I. J. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. C. Courville, and Y. Bengio, “Generative adversarial nets,” in NeurIPS, 2014.
-
X. Chen, Y. Duan, R. Houthooft, J. Schulman, I. Sutskever, and P. Abbeel, “InfoGAN: Interpretable representation learning by informa- tion maximizing generative adversarial nets,” in NeurIPS, 2016.
-
J.Zhu,R.Zhang,D.Pathak,andT.Darrell,“Towardmultimodalimage- to-image translation,” in NeurIPS, 2017.
-
Y. Huang, H. Bi, Z. Li, T. Mao, and Z. Wang, “STGAT: Modeling spatial-temporal interactions for human trajectory prediction,” in ICCV, 2019.
-
A.Mohamed,K.Qian,M.Elhoseiny,andC.Claudel,“Social-STGCNN: A social spatio-temporal graph convolutional neural network for human trajectory prediction,” in CVPR, 2020.
-
P. Velic ̆kovic ́, G. Cucurull, A. Casanova, A. Romero, P. Lio`, and Y. Bengio, “Graph attention networks,” in ICLR, 2018.
-
K. Parth and A. Alexandre, “Adversarial loss for human trajectory prediction,” in hEART, 2019.